The goal of splinetrials is to analyze longitudinal clinical data applying natural cubic splines to a continuous time variable.

Installation

Install this package from CRAN with:

install.packages("splinetrials")

You can also install the development version of splinetrials from GitHub with:

# install.packages("pak")
pak::pak("NikKrieger/splinetrials")

Methods

The NCS model is a longitudinal mixed model of repeated measures (MMRM) with random effects marginalized out, additive baseline covariates, and time parameterized using natural cubic splines. The parameterization has additive effects and pairwise interactions for study arm and time point (i.e., spline basis functions). The model is constrained so that all study arms have equal means at baseline.

Data

We begin with a clinical data set with one row per patient per scheduled visit (including baseline). The following simulated data set represents the general structure (e.g. column names) but not necessarily realistic responses.

set.seed(1)
library(dplyr)
#> 
#> Attaching package: 'dplyr'
#> The following objects are masked from 'package:stats':
#> 
#>     filter, lag
#> The following objects are masked from 'package:base':
#> 
#>     intersect, setdiff, setequal, union
data <-
  mutate(
    cross_join(
      data.frame(
        patient = do.call(paste0, expand.grid(LETTERS, letters))[1:50],
        arm =
          sample(c("control", "active1", "active2"), 50, replace = TRUE),
        categorical1 = sample(paste0("level", 1:3), 50, replace = TRUE),
        categorical2 = sample(c("level1", "level2"), 50, replace = TRUE),
        continuous1 = rnorm(50),
        continuous2 = rnorm(50)
      ),
      data.frame(
        time_observed_index = seq_len(8),
        time_scheduled_index = seq_len(8),
        time_scheduled_label =
          c("Baseline", paste("visit", c(3, 4, 5, 7, 8, 9, 12))),
        time_scheduled_continuous = seq(from = 0, length.out = 8) / 4
      )
    ),
    time_observed_continuous =
      time_scheduled_continuous + runif(n(), min = -0.1, max = 0.1),
    response =
      rnorm(
        n(),
        10 - (1 * (arm == "active1") + 2 * (arm == "active2") +
                3 * (arm == "control")) * sqrt((time_observed_index / 4) -
                                                 min(time_observed_index / 4))
      )
  )

head(data)
#>   patient     arm categorical1 categorical2 continuous1 continuous2
#> 1      Aa control       level3       level2   0.6466744  -0.9106807
#> 2      Aa control       level3       level2   0.6466744  -0.9106807
#> 3      Aa control       level3       level2   0.6466744  -0.9106807
#> 4      Aa control       level3       level2   0.6466744  -0.9106807
#> 5      Aa control       level3       level2   0.6466744  -0.9106807
#> 6      Aa control       level3       level2   0.6466744  -0.9106807
#>   time_observed_index time_scheduled_index time_scheduled_label
#> 1                   1                    1             Baseline
#> 2                   2                    2              visit 3
#> 3                   3                    3              visit 4
#> 4                   4                    4              visit 5
#> 5                   5                    5              visit 7
#> 6                   6                    6              visit 8
#>   time_scheduled_continuous time_observed_continuous  response
#> 1                      0.00               0.07296151 10.685015
#> 2                      0.25               0.18543891 11.766415
#> 3                      0.50               0.49866375  8.439280
#> 4                      0.75               0.73594267  7.332906
#> 5                      1.00               1.01285277  6.027557
#> 6                      1.25               1.28123246  6.099311

The following is a summary of the required columns in the data set. Here are the columns not related to time points or visits:

response: User-supplied numeric vector of responses to the clinical endpoint. Could be AVAL.
patient: User-supplied character vector, ID of the patient in the study. Usually USUBJID.
arm: User-supplied character vector, study arm of the given patient.
categorical1, categorical2: User-supplied example categorical baseline covariates.
continuous1, continuous2: User-supplied example continuous baseline covariates.

Here are the columns related to time points or visits:

time_observed_continuous: User-supplied numeric vector of continuous times corresponding to each observed patient visit. Varies from patient to patient. Units could be in years, months, or days, or some other unit. Must be on the same time scale as time_scheduled_continuous. (If the former is in weeks, then the latter must also be in weeks.)
time_observed_index: User-supplied integer index vector of bins of observed time points. These numeric labels should indicate groupings of time points based on rounding time_observed_continuous to a small set of strategic fixed time points.
time_observed_factor: Derived ordered factor version of time_observed_index to structure the correlation matrix. Derived as ordered(as.character(time_observed_index), levels = as.character(sort(unique(time_observed_index)))).
time_scheduled_index: User-supplied integer index vector of scheduled visit numbers. Usually AVISITN.
time_scheduled_label: User-supplied character vector of human-readable scheduled visit labels. Usually AVISIT.
time_scheduled_continuous: User-supplied numeric vector of continuous times of when each visit was scheduled. It must be on the same time scale as time_scheduled_continuous, the values must have a one-to-one correspondence with the scheduled visits in time_scheduled_label, and the baseline must have a value of 0. If the time scale is weeks, then the study team can create this variable in advance using time_scheduled_label (e.g. AVISIT). For example, if AVISIT is "Baseline", then time_scheduled_continuous must be 0. If time_scheduled_label is "Visit Number 5 (Week 24)", then time_scheduled_continuous should be 24.

Main analysis

The NCS analysis is a call to a single function: ncs_analysis(). This produces a table of summary statistics, including LS means and confidence intervals. All arguments to ncs_analysis() should be exposed as user inputs.

library(splinetrials)
results_table <- ncs_analysis(
  data = data,
  response = "response",
  subject = "patient",
  arm = "arm",
  control_group = "control",
  time_observed_continuous = "time_observed_continuous",
  time_observed_index = "time_observed_index",
  time_scheduled_continuous = "time_scheduled_continuous",
  time_scheduled_label = "time_scheduled_label",
  covariates = ~ continuous1 + categorical2,
  cov_structs = c("us", "toeph", "ar1h", "csh", "cs"),
  df = 3
)

results_table
#> # A tibble: 24 × 32
#>    arm     time         n   est    sd    se lower upper response_est response_se
#>    <fct>   <chr>    <int> <dbl> <dbl> <dbl> <dbl> <dbl>        <dbl>       <dbl>
#>  1 active1 Baseline    19 10.0  1.04  0.240  9.57 10.5          9.95       0.127
#>  2 active1 visit 3     19  9.13 0.909 0.208  8.72  9.54         9.40       0.105
#>  3 active1 visit 4     19  9.02 1.10  0.253  8.53  9.52         8.94       0.144
#>  4 active1 visit 5     19  9.08 0.969 0.222  8.65  9.52         8.69       0.138
#>  5 active1 visit 7     19  8.57 1.17  0.268  8.05  9.10         8.63       0.134
#>  6 active1 visit 8     19  8.72 0.861 0.198  8.34  9.11         8.70       0.150
#>  7 active1 visit 9     19  9.16 1.21  0.278  8.61  9.70         8.84       0.126
#>  8 active1 visit 12    19  8.83 0.851 0.195  8.45  9.21         9.03       0.183
#>  9 active2 Baseline    13 10.3  0.883 0.245  9.82 10.8          9.95       0.127
#> 10 active2 visit 3     13  8.49 1.10  0.304  7.90  9.09         9.19       0.120
#> # ℹ 14 more rows
#> # ℹ 22 more variables: response_df <dbl>, response_lower <dbl>,
#> #   response_upper <dbl>, change_est <dbl>, change_se <dbl>, change_df <dbl>,
#> #   change_lower <dbl>, change_upper <dbl>, change_test_statistic <dbl>,
#> #   change_p_value <dbl>, diff_est <dbl>, diff_se <dbl>, diff_df <dbl>,
#> #   diff_lower <dbl>, diff_upper <dbl>, diff_test_statistic <dbl>,
#> #   diff_p_value <dbl>, percent_slowing_est <dbl>, …

The table has one row per study arm per timepoint of interest and the following columns.

arm: study arm, i.e. treatment group
time: discrete visit time labels from the time_scheduled_label column in the data.
n: number of non-missing observations.
est: observed mean response in the data.
sd: observed standard deviation of the response in the data.
se: observed standard error of the response in the data (just se / sqrt(n)).
lower: lower bound of an observed 95% confidence interval in the data.
upper: upper bound of an observed 95% confidence interval in the data.
response_est: LS mean of the response.
response_se: standard error of the LS mean of the response.
response_df: degrees of freedom of the LS mean of the response.
response_lower: lower 95% confidence bound of the LS mean of the response.
response_upper: upper 95% confidence bound of the LS mean of the response.
change_est, change_lower, change_upper, change_se, change_df: like the analogous response_* columns, but for LS mean change from baseline.
change_test_statistic: test statistic of a two-sided test that the LS mean change from baseline is not equal to 0, at a significance level of 5%.
change_p_value: same as change_test_statistic, but the p-value instead of the test statistic.
diff_est, diff_se, diff_df, diff_lower, diff_upper, diff_test_statistic, diff_p_value: same as the analogous change_* columns, but for treatment differences.
percent_slowing_est LS mean of percent slowing (on the percentage scale).
percent_slowing_lower, percent_slowing_upper: a conservative approximation to a confidence interval on percent slowing. Assumes uncorrelated changes from baseline.
correlation: correlation structure of the whole model.
optimizer: optimization algorithm for the whole model.

We can plot the model against the data.

ncs_plot_means(results_table)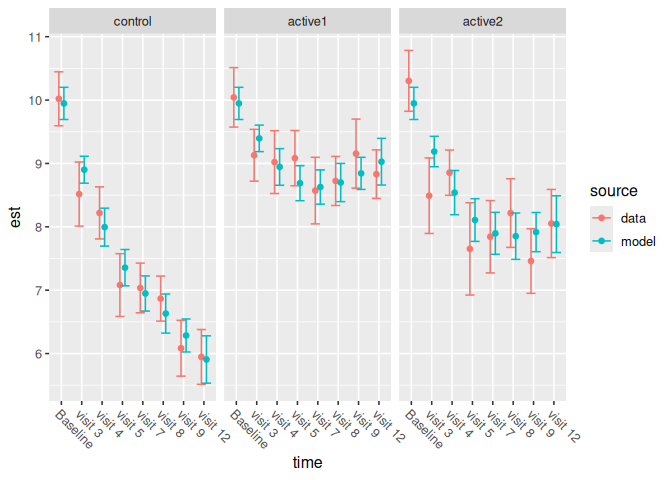

Subgroup analysis

The subgroup analysis is similar, but it begins with a data set with a categorical variable column to indicate subgroup membership.

set.seed(1)
data_with_subgroup <-
  mutate(
    cross_join(
      data.frame(
        patient = do.call(paste0, expand.grid(LETTERS, letters))[1:120],
        arm = rep(c("control", "active1", "active2"), each = 40),
        subgroup = rep(c("subgroup1", "subgroup2", "subgroup3"), times = 40),
        categorical1 = sample(paste0("level", 1:3), 120, replace = TRUE),
        categorical2 = sample(c("level1", "level2"), 120, replace = TRUE),
        continuous1 = rnorm(120),
        continuous2 = rnorm(120)
      ),
      data.frame(
        time_observed_index = seq_len(8),
        time_scheduled_index = seq_len(8),
        time_scheduled_label =
          c("Baseline", paste("visit", c(3, 4, 5, 7, 8, 9, 12))),
        time_scheduled_continuous = as.numeric(seq(from = 0, length.out = 8) / 4)
      )
    ),
    time_observed_continuous =
      time_scheduled_continuous + runif(n(), min = -0.1, max = 0.1),
    response = rnorm(
      n(),
      mean =
        10 - (1 * (arm == "active1") + 2 * (arm == "active2") +
                3 * (arm == "control")) * sqrt((time_observed_index / 4) -
                                                 min(time_observed_index / 4))
    )
  )

head(data_with_subgroup)
#>   patient     arm  subgroup categorical1 categorical2 continuous1 continuous2
#> 1      Aa control subgroup1       level1       level1  -0.9568919   0.6060734
#> 2      Aa control subgroup1       level1       level1  -0.9568919   0.6060734
#> 3      Aa control subgroup1       level1       level1  -0.9568919   0.6060734
#> 4      Aa control subgroup1       level1       level1  -0.9568919   0.6060734
#> 5      Aa control subgroup1       level1       level1  -0.9568919   0.6060734
#> 6      Aa control subgroup1       level1       level1  -0.9568919   0.6060734
#>   time_observed_index time_scheduled_index time_scheduled_label
#> 1                   1                    1             Baseline
#> 2                   2                    2              visit 3
#> 3                   3                    3              visit 4
#> 4                   4                    4              visit 5
#> 5                   5                    5              visit 7
#> 6                   6                    6              visit 8
#>   time_scheduled_continuous time_observed_continuous response
#> 1                      0.00              -0.07428706 9.336270
#> 2                      0.25               0.23840196 9.916441
#> 3                      0.50               0.43845954 6.507177
#> 4                      0.75               0.73698012 7.510785
#> 5                      1.00               0.94502668 6.533178
#> 6                      1.25               1.34221926 9.607641

For completeness, here is a full description of the columns in the data. Columns not related to time points or visits:

subgroup: User-supplied character vector indicating the subgroup of each patient.
response: User-supplied numeric vector of responses to the clinical endpoint. Could be AVAL.
patient: User-supplied character vector, ID of the patient in the study. Usually USUBJID.
arm: User-supplied character vector, study arm of the given patient.
categorical1, categorical2: User-supplied example categorical baseline covariates.
continuous1, continuous2: User-supplied example continuous baseline covariates.

Columns related to time points and visits:

time_observed_continuous: User-supplied numeric vector of continuous times corresponding to each observed patient visit. Varies from patient to patient. Units could be in years, months, or days, or some other unit. Must be on the same time scale as time_scheduled_continuous. (If the former is in weeks, then the latter must also be in weeks.)
time_observed_index: User-supplied integer index vector of bins of observed time points. These numeric labels should indicate groupings of time points based on rounding time_observed_continuous to a small set of strategic fixed time points.
time_observed_factor: Derived ordered factor version of time_observed_index to structure the correlation matrix. Derived as ordered(as.character(time_observed_index), levels = as.character(sort(unique(time_observed_index)))).
time_scheduled_index: User-supplied integer index vector of scheduled visit numbers. Usually AVISITN.
time_scheduled_label: User-supplied character vector of human-readable scheduled visit labels. Usually AVISIT.
time_scheduled_continuous: User-supplied numeric vector of continuous times of when each visit was scheduled. It must be on the same time scale as time_scheduled_continuous, the values must have a one-to-one correspondence with the scheduled visits in time_scheduled_label, and the baseline must have a value of 0. If the time scale is weeks, then the study team can create this variable in advance using time_scheduled_label (e.g. AVISIT). For example, if AVISIT is "Baseline", then time_scheduled_continuous must be 0. If time_scheduled_label is "Visit Number 5 (Week 24)", then time_scheduled_continuous should be 24.

The NCS subgroup analysis is a call to a single function: ncs_analysis_subgroup(). This produces a table of summary statistics, including LS means and confidence intervals.

subgroup_results <-
  ncs_analysis_subgroup(
    data = data_with_subgroup,
    response = "response",
    subject = "patient",
    arm = "arm",
    control_group = "control",
    subgroup = "subgroup",
    subgroup_comparator = "subgroup1",
    time_observed_continuous = "time_observed_continuous",
    time_observed_index = "time_observed_index",
    time_scheduled_continuous = "time_scheduled_continuous",
    time_scheduled_label = "time_scheduled_label",
    covariates = ~ continuous1 + categorical2,
    cov_structs = c("us", "toeph", "ar1h", "csh", "cs"),
    df = 3
  )

We can plot the model against the data.

ncs_plot_means_subgroup(subgroup_results$within)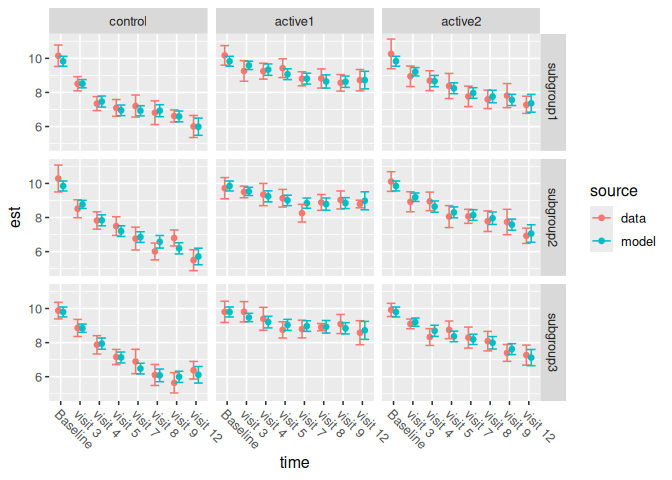

Between-subgroup table:

subgroup_results$between
#> # A tibble: 72 × 30
#>    arm     time     subgroup      n   est    sd    se lower upper response_est
#>    <fct>   <chr>    <fct>     <int> <dbl> <dbl> <dbl> <dbl> <dbl>        <dbl>
#>  1 active1 Baseline subgroup1    13 10.2  1.05  0.292  9.60 10.7          9.83
#>  2 active1 Baseline subgroup2    14  9.72 1.19  0.317  9.10 10.3          9.85
#>  3 active1 Baseline subgroup3    13  9.81 1.14  0.317  9.18 10.4          9.80
#>  4 active2 Baseline subgroup1    13 10.3  1.60  0.444  9.39 11.1          9.83
#>  5 active2 Baseline subgroup2    13 10.1  1.06  0.295  9.53 10.7          9.85
#>  6 active2 Baseline subgroup3    14  9.92 0.741 0.198  9.53 10.3          9.80
#>  7 control Baseline subgroup1    14 10.2  1.20  0.320  9.52 10.8          9.83
#>  8 control Baseline subgroup2    13 10.3  1.45  0.402  9.50 11.1          9.85
#>  9 control Baseline subgroup3    13  9.88 0.896 0.249  9.39 10.4          9.80
#> 10 active1 visit 3  subgroup1    13  9.26 1.11  0.307  8.66  9.86         9.59
#> # ℹ 62 more rows
#> # ℹ 20 more variables: response_se <dbl>, response_df <dbl>,
#> #   response_lower <dbl>, response_upper <dbl>, change_est <dbl>,
#> #   change_se <dbl>, change_df <dbl>, change_lower <dbl>, change_upper <dbl>,
#> #   change_test_statistic <dbl>, change_p_value <dbl>, diff_subgroup_est <dbl>,
#> #   diff_subgroup_se <dbl>, diff_subgroup_df <dbl>, diff_subgroup_lower <dbl>,
#> #   diff_subgroup_upper <dbl>, diff_subgroup_test_statistic <dbl>, …

Within-subgroup table:

subgroup_results$within
#> # A tibble: 72 × 33
#>    arm     time     subgroup      n   est    sd    se lower upper response_est
#>    <fct>   <chr>    <fct>     <int> <dbl> <dbl> <dbl> <dbl> <dbl>        <dbl>
#>  1 active1 Baseline subgroup1    13 10.2  1.05  0.292  9.60 10.7          9.83
#>  2 active1 visit 3  subgroup1    13  9.26 1.11  0.307  8.66  9.86         9.59
#>  3 active1 visit 4  subgroup1    13  9.25 0.856 0.237  8.78  9.71         9.34
#>  4 active1 visit 5  subgroup1    13  9.42 1.01  0.280  8.87  9.97         9.07
#>  5 active1 visit 7  subgroup1    13  8.80 0.762 0.211  8.39  9.22         8.81
#>  6 active1 visit 8  subgroup1    13  8.82 1.03  0.286  8.26  9.38         8.64
#>  7 active1 visit 9  subgroup1    13  8.56 0.893 0.248  8.08  9.05         8.63
#>  8 active1 visit 12 subgroup1    13  8.72 1.15  0.319  8.09  9.34         8.72
#>  9 active2 Baseline subgroup1    13 10.3  1.60  0.444  9.39 11.1          9.83
#> 10 active2 visit 3  subgroup1    13  8.95 1.10  0.306  8.35  9.55         9.21
#> # ℹ 62 more rows
#> # ℹ 23 more variables: response_se <dbl>, response_df <dbl>,
#> #   response_lower <dbl>, response_upper <dbl>, change_est <dbl>,
#> #   change_se <dbl>, change_df <dbl>, change_lower <dbl>, change_upper <dbl>,
#> #   change_test_statistic <dbl>, change_p_value <dbl>, diff_arm_est <dbl>,
#> #   diff_arm_se <dbl>, diff_arm_df <dbl>, diff_arm_lower <dbl>,
#> #   diff_arm_upper <dbl>, diff_arm_test_statistic <dbl>, …

The between-subgroup and within-subgroup tables have one row per study arm per timepoint per subgroup and the following columns.

arm: study arm, i.e. treatment group
time: discrete visit time labels from the time_scheduled_label column in the data.
subgroup: subgroup level
n: number of non-missing observations.
est: observed mean response in the data.
sd: observed standard deviation of the response in the data.
se: observed standard error of the response in the data (just se / sqrt(n)).
lower: lower bound of an observed 95% confidence interval in the data.
upper: upper bound of an observed 95% confidence interval in the data.
response_est: LS mean of the response.
response_se: standard error of the LS mean of the response.
response_df: degrees of freedom of the LS mean of the response.
response_lower: lower 95% confidence bound of the LS mean of the response.
response_upper: upper 95% confidence bound of the LS mean of the response.
change_est, change_lower, change_upper, change_se, change_df: like the analogous response_* columns, but for LS mean change from baseline.
change_test_statistic: test statistic of a two-sided test that the LS mean change from baseline is not equal to 0, at a significance level of 5%.
change_p_value: same as change_test_statistic, but the p-value instead of the test statistic.
diff_arm_est, diff_arm_se, diff_arm_df, diff_arm_lower, diff_arm_upper, diff_arm_test_statistic, diff_arm_p_value: same as the analogous change_* columns, but for treatment differences.
diff_subgroup_est, diff_subgroup_se, diff_subgroup_df, diff_subgroup_lower, diff_subgroup_upper, diff_subgroup_test_statistic, diff_subgroup_p_value: same as the analogous *_arm_* columns, but for the subgroup differences.
percent_slowing_est LS mean of percent slowing (on the percentage scale).
percent_slowing_lower, percent_slowing_upper: a conservative approximation to a confidence interval on percent slowing. Assumes uncorrelated changes from baseline.
correlation: correlation structure of the analysis subgroup model.
optimizer: optimizer of the analysis subgroup model.

Type-III ANOVA fixed effects:

subgroup_results$type3
#> # A tibble: 15 × 6
#>    effect            chisquare_test_stati…¹    df  p_value correlation optimizer
#>    <chr>                              <dbl> <int>    <dbl> <chr>       <chr>    
#>  1 spline_fn(time_o…               134.         1 4.36e-31 heterogene… mmrm+tmb 
#>  2 spline_fn(time_o…               342.         1 2.23e-76 heterogene… mmrm+tmb 
#>  3 spline_fn(time_o…               189.         1 6.16e-43 heterogene… mmrm+tmb 
#>  4 subgroup                          0.0641     2 9.68e- 1 heterogene… mmrm+tmb 
#>  5 continuous1                       1.72       1 1.90e- 1 heterogene… mmrm+tmb 
#>  6 categorical2                      0.958      1 3.28e- 1 heterogene… mmrm+tmb 
#>  7 spline_fn(time_o…                 0.770      2 6.80e- 1 heterogene… mmrm+tmb 
#>  8 spline_fn(time_o…                 0.189      2 9.10e- 1 heterogene… mmrm+tmb 
#>  9 spline_fn(time_o…                 0.514      2 7.73e- 1 heterogene… mmrm+tmb 
#> 10 spline_fn(time_o…                24.7        2 4.26e- 6 heterogene… mmrm+tmb 
#> 11 spline_fn(time_o…               376.         2 2.02e-82 heterogene… mmrm+tmb 
#> 12 spline_fn(time_o…                42.0        2 7.62e-10 heterogene… mmrm+tmb 
#> 13 spline_fn(time_o…                13.9        4 7.74e- 3 heterogene… mmrm+tmb 
#> 14 spline_fn(time_o…                 2.62       4 6.23e- 1 heterogene… mmrm+tmb 
#> 15 spline_fn(time_o…                 2.54       4 6.37e- 1 heterogene… mmrm+tmb 
#> # ℹ abbreviated name: ¹chisquare_test_statistic

There is also a table for the subgroup interaction test:

subgroup_results$interaction
#>           model      aic      bic    loglik -2*log(l) test_statistic df
#> 1 reduced model 2884.131 3040.231 -1386.066  2772.131             NA NA
#> 2    full model 2891.246 3080.796 -1377.623  2755.246       16.88529 12
#>     p_value                correlation optimizer
#> 1        NA heterogeneous unstructured  mmrm+tmb
#> 2 0.1539634 heterogeneous unstructured  mmrm+tmb

The test itself is a likelihood ratio test between a full model with subgroup-treatment interaction and a reduced model without subgroup-treatment interaction. The table has a row for the full model, a row for the reduced model, and the following columns.

model: the model, either full or reduced.
df: degrees of freedom
aic: Akaike Information Criterion
bic: Bayesian Information Criterion
loglik: log likelihood
test_statistic: test statistic of the likelihood ratio test.
p_value: p-value of the likelihood ratio test.
correlation: correlation structures of the full and reduced models of the interaction test.
optimizer: optimizers of the full and reduced models of the interaction test.